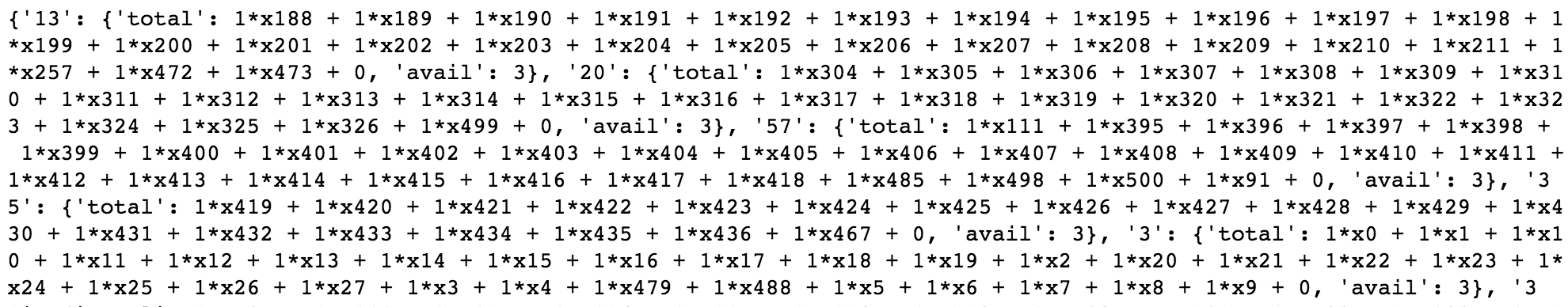Intro

Having been invited by many people in many social circles to participate in a Fantasy Football League, I decided to take 30 minutes out of my day to approach it like I would any problem... with the data! In this post, I detail how I employed the simplex method, a linear optimisation technique, that looks to optimise an objective function with respect to a number of constraints in a linear manner. I thought I would share with you the process I went through, both to hopefully get feedback on how I can improve for next year when I try select a new team and hopefully have more data sources and to help people see the endless application of analytics to help inform decisions!
"Keep it Plain & Simplex" comes from the method that I adopt, the "simplex method" and a style of football every coach I have ever had shout out to my teamates and I... "Keep it simple! Simple passes"!

Description

I enjoy playing games and taking part in activities and sports, not necessarily watching other people! It's this mentality that has led to me falling out of touch with the latest in football today (besides FIFA of course, because I'd be "playing"). However, I do have many friends and colleagues that are avid fans of the sport and extend their fandom to fantasy football! Fantasy football is a big part of the footballing community as this gives them the chance to participate in leagues and use their expert knowledge of players and their performance to out-perform their piers, and even perhaps win some money at the same time, and of course win the pride that comes along with besting others at a feat and be known as a football guru.
There is no way I would ever make such a bold claim as to be a football guru, but what I can confidently say is that I am a data guru! As you can tell by my blog, I love data and the analytics that can be done with it. So when I was approached by my colleagues and my friends in the coming weeks to the deadline, I stayed strong and decided not to participate until about 30 minutes to the deadline! I thought to myself "Why Not?!", it's free! Apart from the damage to my reputation as a football guru! but seeing as that was non-existent, I figured it was a calculated risk.

​There was no way I was going to read up on all the latest transfers and all the possible bits of information about the footballers in the time that I had, however, the fantasy site gives you data about the players and their performance based on last season, so I went with that and dived into the data and leveraged that to make my decision for me!

Rules

So the first thing I did was familiarise myself with the rules. After conducting a bit of research, I came to the following conclusions that would inform the analytical approach I would use to make my decision.
  • Each week, players earn points based on their performance in games throughout the week;
  • The aim of the game is to pick players whom you think will  earn the most points in the season;
  • You are constrained to a budget of £100.0 million to choose players (better players cost more money);
  • You must pick 15 players, 2 goal keepers, 5 defenders, 5 midfielders and 3 strikers;
  • Only 11 players must be on the pitch (1 goalkeeper - 4 defenders - 4 midfielders - 2 strikers), and 4 on the bench (1-1-1-1);
  • You can only pick up to 3 players from any given team;
  • Only the 11 players selected to play can earn points each week.

Approach

With this in mind, I decided to take the approach of selecting the best 11 players possible with regards to my cost and other constraints; and from there purchase the highest earning remaining 4 based on the cheapest players. With all this in mind, it sounds like i need to:
  1. Optimise the number of points I can get (objective function)
  2. Make sure I had 15 players (constraint 1)
  3. Make sure I had 2 goalkeepers (constraint 2)
  4. Make sure I had 5 defenders (constraint 3)
  5. Make sure I had 5 midfielders (constraint 4)
  6. Make sure I had 3 strikers (constrain 5)
  7. Make sure I spent less than £100.0 million (constraint 6)
  8. Make sure I select between 0 and 3 players from any given team
This sounds a lot like a linear programming problem (LPP) and so that's exactly how I looked to optimise the problem! I decided to look at this problem as a system of linear equations of which I could optimise an objective function with respect to a number of constraints. I decided to use a Linear Optimisation technique called the simplex method (Hence the name in the title). 

Imports


    









So, lets dive right into the data now that we've download the json file from the fantasy website with all the data from last year and imported all the packages we need to analyse the data. There are a number of different levels to the JSON with different data in each but our main concern is the player data which is held within the 'elements' section.










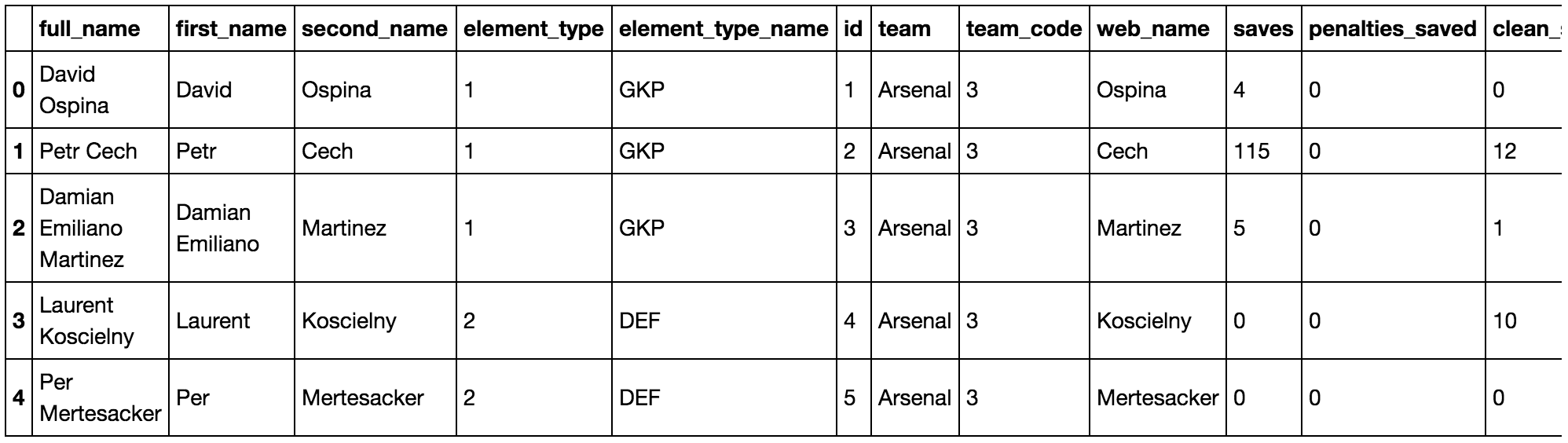
Player Data




	

    

        

    

    

        

    









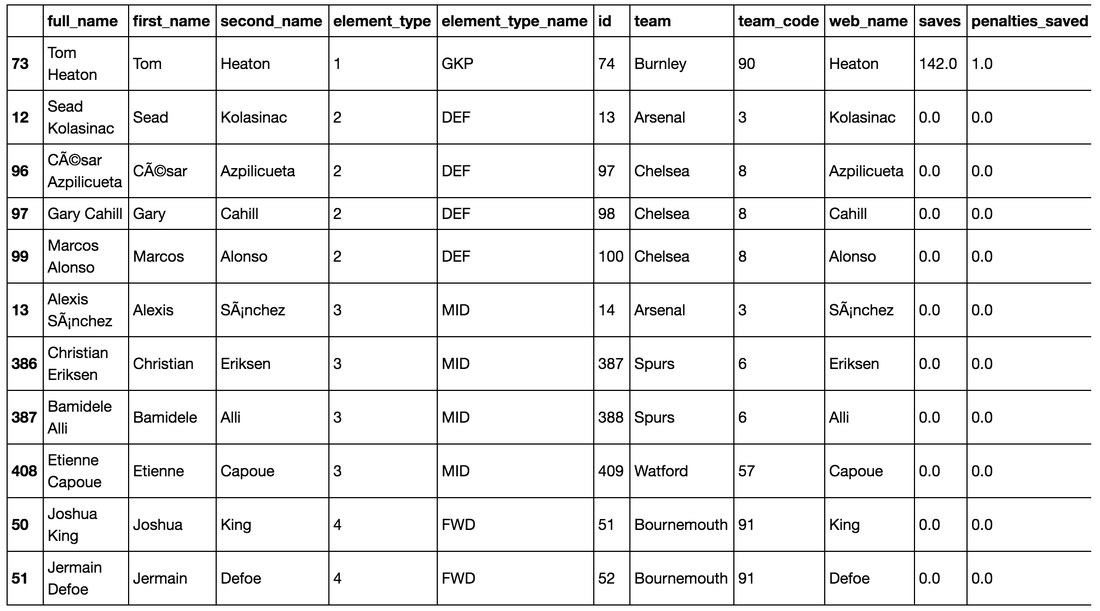
Here we can see that there are a number of features in the dataset. We can clean up this data to only consider the features that we're interested in. I also concatenate the names of the players in order to better identify players in one column. I have mapped each players position and teams, from other areas of the original json file, to make a more comprehensive dataset.












Explore




	

    

        

    

    

        

    









Out of curiosity, I wanted to see what features were correlated to the total points a player earned in the season. Here we can see that the points won are highly correlated to:
  • clean sheets - players with more clean sheets tend to score more points.
  • bps - players that earned more points in the bonus points system earned more points
  • minutes - players that played more minutes tend to score more points.
  • goals conceded - interestingly, the more goals players conceded the more points they earned. I think this may be driven by the minutes variable in that a player is likely to score points by actually playing and in turn are more likely to concede goals. If a player does not play, they have no chance to concede goals and they are also not able to score points.



Digging deeper to understand a bit more about the data, looking at the average and median scores of players by there position, it is clear that on average forwards earn more points than any other position and goal keepers earn the least. However, looking at the counts of players, there are far more midfielders and defenders than there are forwards and goalkeepers, so this should be kept in mind when drawing conclusions about the data.












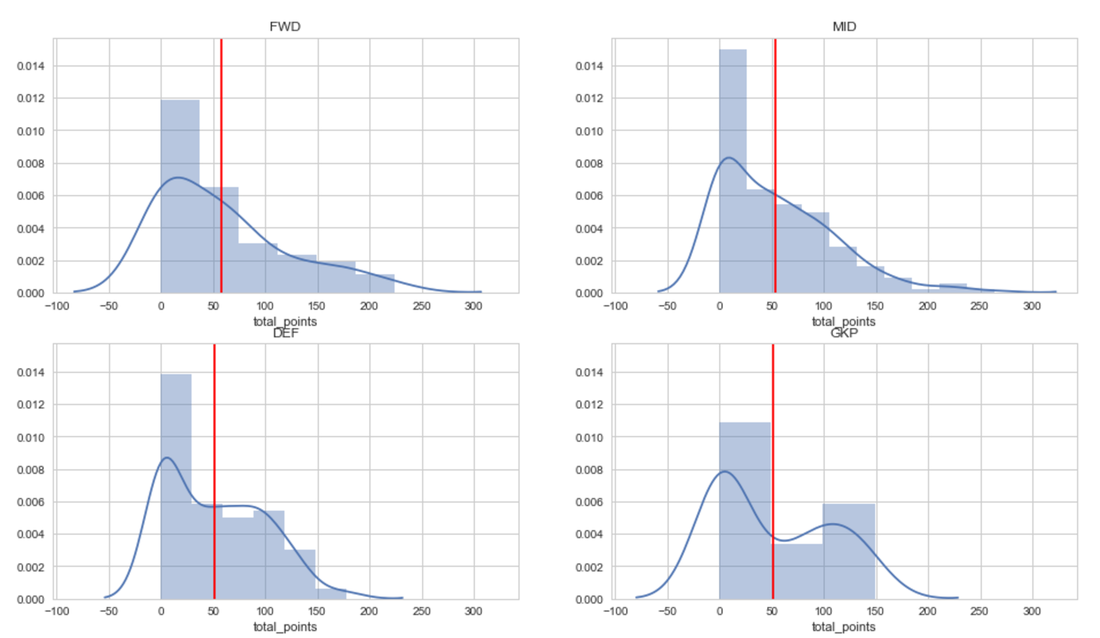
Kernel Density Estimation




	

    

        

    

    

        

    









Given the differences in counts, i thought it would be a good idea to have a look at some kernel density estimations to show the distribution of points based on the position of the players. This should give more of an indication as to the distribution of points for each position. Most of the data is positively skewed and slightly leptokertic, however, the goalkeeper distribution seems to be bimodal. This would make sense as most clubs will have 2-3 goalkeepers at a time and will play the better goalkeeper the majority of the time resulting in more time to earn points and the other 0 to few games as the others would only be switched in times of need when the 1st choice keeper is injured or needs to be rested.












Imputations



The reason for this positive skew and leptokurtic data is due to players that had been transferred into the premier league that had no historic data and players that earned no points in the previous season. This is one of the limitations of the data. With no data about the historic performance of these players it would be difficult to judge their performance and really pick the best options for the season.
This also highlights the naivety of the approach I have adopted in that I make assumptions that players will replicate similar performance this season as to last season. Essentially, I would like to select some of the newly transferred players as I can imagine they would be out to try and impress and potentially perform better.



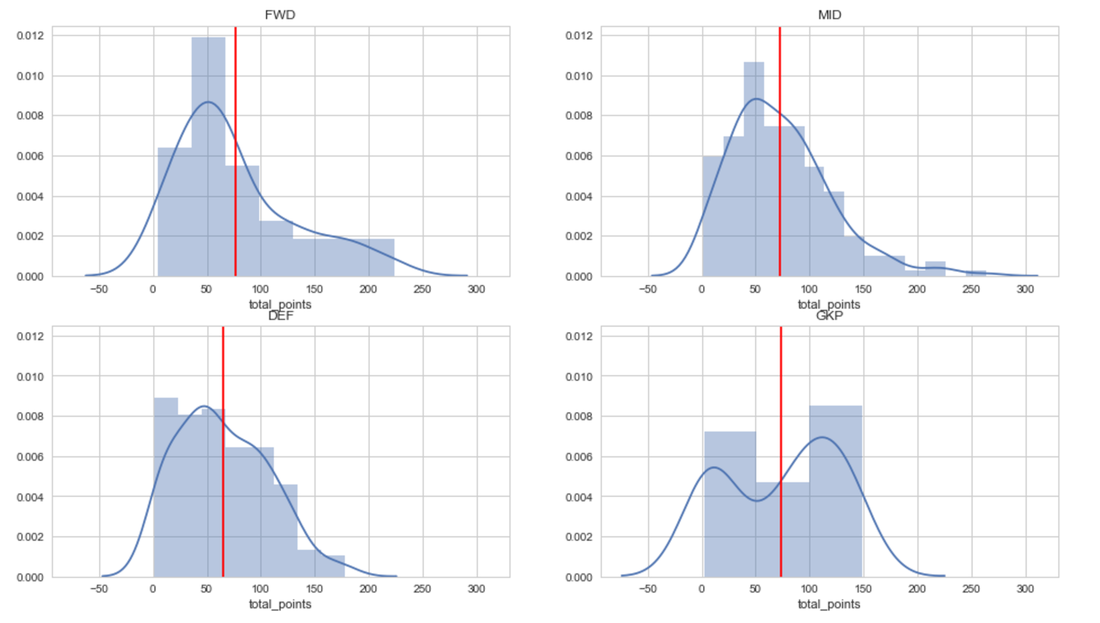
The way I decided to go about making this data usable and make the new transfers available  is imputing data. I assigned values to each of the players based on their cost. I would use the average or median of the particular stat based on the players of the same costs and same position and impute the values from there. I would then add a bit of gaussian noise multiplied by the standard deviation of the given feature to the imputed values to "simulate" random performance chances for the players with no data and to add some variance to the dataset because there are a large number of 0 scoring players (25.55%). I used a controlled gaussian by dividing by 1.5 to ensure that the variance isn't too erratic.




	

    

        

    

    

        

    









Here I use a number of nested loops to store the medians and standard deviations specific to the position and cost of a player based on the featured columns. I make sure to use the absolute value as to avoid negative imputations and to help skew the data to a more normal distribution and remain consistent with the assumption that transferred players will be looking to perform well to impress. I softened the gaussian noise just a bit to avoid erratic data. After the imputation I then visualised the distributions and kernel density estimations and the data begins to resemble a gaussian curve, except the goalkeeper estimation which appears to remain bimodal.












Linear Modelling



Now that I have my dataset ready, it's time for me to model the problem into the system of linear elements. I will start by modelling the problem to select the best possible 11 players that I can with as much money as I can afford to use. To model the problem in python, I will be using Pulp. Pulp is a python package that is able to model linear optimisation problems and solve them using the simplex method. For more info on pulp, there are a number of resources online that you can access. I import everything from pulp and declare my Linear Programming problem and name it "Fantasy Team" and indicate that it is a maximising linear programming problem as I will be looking to maximise the number of points that I can get.




	

    

        

    

    

        

    
















Decision Variables



I decided to use each of the available players as the decision variables where their values will be binary in that I will choose them (1) or I wont (0). This is achieved using the following code below, casting the variables as integer variables. There are 501 players for me to choose from therefore there are 501 decision variables.




	

    

        

    

    

        

    
















Optimisation Function



Here is where I assign the optimisation function. This is what I am trying to maximise as previously stated in my modelling of the problem. Each player earned a given number of points in the previous season, or they have been imputed with values based on the median + (soft gaussian noise * standard deviation) dependant on the given cost and position of that player and other players within that cost bracket in the same position. These are taken and assigned to each of the decision variables (players) and used to construct the function as shown below.




	

    

        

    

    

        

    


















Cash Constraint



Here is where I assign the cash constraint. Remembering that we only have £100.0million (1000 in code) to spend on the whole squad, and my tactic to pick the best 11 based on the available cash I had after buying the best of the cheapest 4 benched players. The cheapest players that I could choose from cost  a total of £17.0million (170 in code). Therefore, this left me with £83.0 million (830 in code) to pick the best performing 11 players. I set the constraint so that I could spend 830 or less on selecting the best 11 players.




	

    

        

    

    

        

    
















Player Constraints



Here is where I assign the constraints based on the number of players that I am going to choose. deciding to go with a traditional 4-4-2 formation, I had the constraints reflect this. What the constraints represent is, of all the decision variables, some are defenders, some are midfielders and some are strikers; make sure that you select 4 defenders, 4 midfielders and 2 strikers.



Goalkeeper Constraint




	

    

        

    

    

        

    









Defender Constraint




	

    

        

    

    

        

    









Midfielder Constraint




	

    

        

    

    

        

    









Forward Constraint




	

    

        

    

    

        

    
















Team Constraint



This was slightly trickier. Here I ensure that up to 3 players from any given team are selected and not any more. To achieve this, I used a hash table to store all the teams and the players (decision variables) within the team where each of their values is equal to 1 so that i am only able to pick as many players as what is available, in this case 3.




	

    

        

    

    

        

    


















Solve



Now that we have put in all our decision variables, constraints and optimisation function, it's time to solve the Linear Programming Problem! This prints all the values of the decision variables with respect to the linear relationships we have highlighted in the modelling process. I have also assert that this result is the optimal result.




	

    

        

    

    

        

    
















Solution



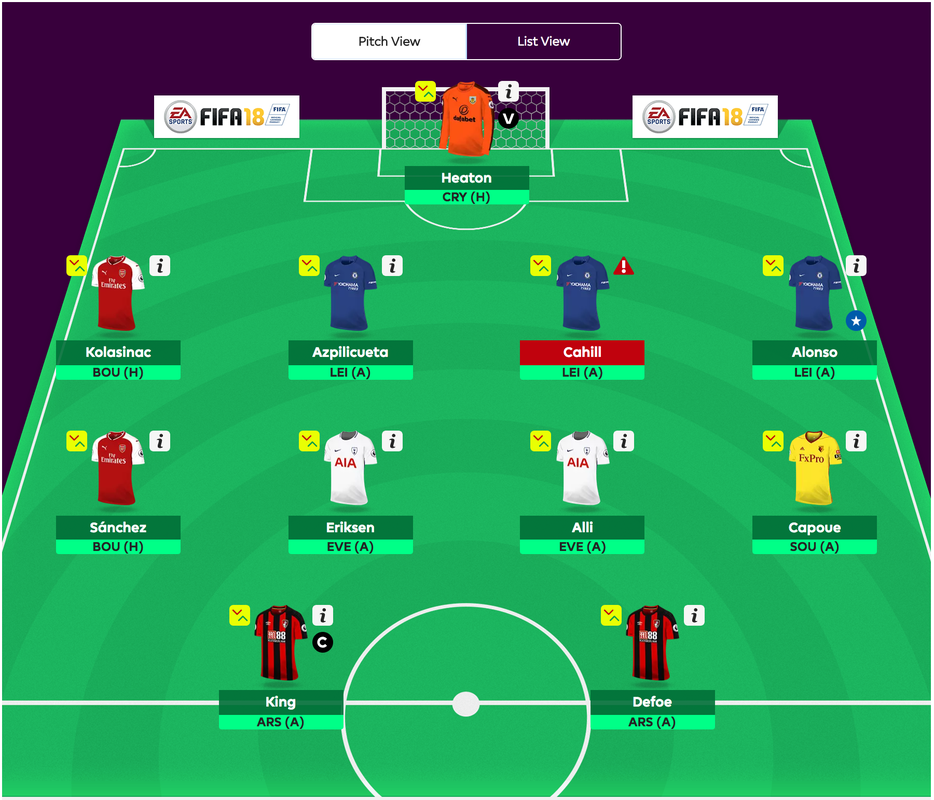
Now to make sense of the results of the problem. I build a pandas dataframe of all the decisions made following the optimisation model and append it to the original dataset to see who has been selected to be in the dream team!




	

    

        

    

    

        

    











Above is the selected dream team. Here we can see that the optimisation algorithm ensured that it adhered to the constraints. There are 4 defenders, 4 midfielders and 2 forwards. It has also maxed out the total available balance to purchase players. And the total score that has been maximised is 2010.86. I'm not sure as to whether that's a great score but lets hope the data is right and I win a few leagues!












Final Thoughts & Ideas...



This was a very quick and abrasive way to approach the problem, given the time that I had to solve it, however, I feel it was a good attempt. Coming into contact with this data for the first time, I was very interested in perhaps clustering or selecting players using other algorithms. One method that comes to mind is highlighting the best forward, midfielder and defender and assigning them the centres of focus and using a k-Nearest Neighbours approach to selecting players that have similar stats to the best but at a much cheaper price to optimise my points and minimise my cost. 

Another approach would be to enrich this data with the use of historical data for each player and using forecasting methods to predict what they will achieve in the next season and use those figures within the Linear Programming Problem.

Let me know what you think? How would YOU approach the problem? Any ideas for me to implement next year to reduce my assumptions and overcome the limitations of the above method?




	

	

		
	









The Jupyter Notebook Repo is Available Here