Description
In the world of data science, I have come to learn that there are thousands of variables that you can choose to help you make your predictions and there are techniques which you can apply to find out which are the best features. I came up with this idea when I had 2000 variables to choose from in order to build a regression model. This left me with 2^2000 potential combinations! I then thought of using an optimisation technique, a genetic algorithm, in order to pick the best features. Of Course this can also be applied to a dataset with far fewer number of features, though it is recommended to use on medium-large datasets though there are hyperparameters that can be adjusted to suit all needs. There are other feature selection techniques that can be used, however, I thought this was an interesting approach and decided to explore it.
Genetic Algorithm
What is a Genetic Algorithm? I will try my best to explain very briefly what it is, how it works and why it works! If even after my explanation, you want to know more about the algorithm, there are a number of resources online that could go into a deeper explanation of genetic algorithms, their origins and how they work at a deeper level, however, that is beyond the scope of this post.
A genetic algorithm is an algorithm (approach or series of steps) that looks to find an optimal solution amongst a pool of solutions, and then builds on the best solutions to then create a new pool of solutions. It then looks to augment the existing pool (also know as mutation) in order to add a random element that could potentially enhance the solutions. It continues in this process, selecting the best of the solutions which over time should produce an optimal or close to optimal solution. This mimics evolution, where it's "survival of the fittest", and based on the "fittest", a new generation of solutions are created. There are a number of variations to the algorithm such as deciding how to generate the new pool based on the existing pool as well as a number of hyperparameters such as the size of the pool, number of iterations and the rate of mutation.
Feature Selection
How does this apply to feature selection in building machine learning models? Well, if you have a large number of features in a dataset, you may not know which is the best combination of features to make the best predictive model. This is where the genetic algorithm can come in handy by hosting a pool of potential combinations of features and running the algorithm as described above. Depending on what type of model you are using, will depend on how you evaluate a model. After however many iterations you choose, the results will be the optimal solution for the genetic algorithm at that point.
To translate my simplified explanation into simplified biological terms (from which this algorithm is inspired), the pool of solutions are chromosomes and chromosomes are made up of genes which are in an order that defines which features to select for that particular solution. In this case, you have a binary option, you can select a feature or you can omit a feature. if the gene representing a single feature is 1 then this feature will be selected and if the gene representing a single feature is 0 then it will not be selected within the dataset.
To translate my simplified explanation into simplified biological terms (from which this algorithm is inspired), the pool of solutions are chromosomes and chromosomes are made up of genes which are in an order that defines which features to select for that particular solution. In this case, you have a binary option, you can select a feature or you can omit a feature. if the gene representing a single feature is 1 then this feature will be selected and if the gene representing a single feature is 0 then it will not be selected within the dataset.
The Code (Less than 150 lines!👍🏾)
My implementation
Above is the code that I will be breaking down. The genetic algorithm has been coded into a class to keep everything tidy within an object. My implementation takes advantage of the standardised approach of the sci-kit learn library and attempts to continue in the same fashion with the .fit() function. Below I will break down my implementation, tying in the theory behind genetic algorithms whilst explaining my reasoning for certain modifications.
Imports
The main imports for the script hosting the genetic algorithm are as shown above. Numpy is a very popular library that I use to take advantage of the speed benefits associated with arrays as well as built in functions that help run the algorithm. The time library is simply used to keep track of the time taken to run each iteration. The sklearn.model_selection imports are used to provide the ability to cross-validate in order to account for any overfitting of models when using the scores within the sklearn.metrics library. I have also included sklearn.decomposition imports in order to increase the speed of iterations using Principal Component Analysis (PCA). I have also included matplotlib to plot the results of the genetic algorithm. All these imports and where they are used in the code will be explained below.
__init__() Method
For the first method in the class, I have obviously started with __init__(). In python, this method is initialised upon the creation of an instance of the class. So when creating the object, I have allowed for 3 hyperparameters to be selected. The first is the "mutation_rate" which is a number between 0 and 1 representing the probability that a gene/feature within a solution will mutate (from 0 to 1 or vice versa). The "iterations" hyperparameter dictates how many generations the algorithm should operate. The final hyper parameter is the "pool_size" which dictates how many solutions should be considered at each iteration.
fit() Method
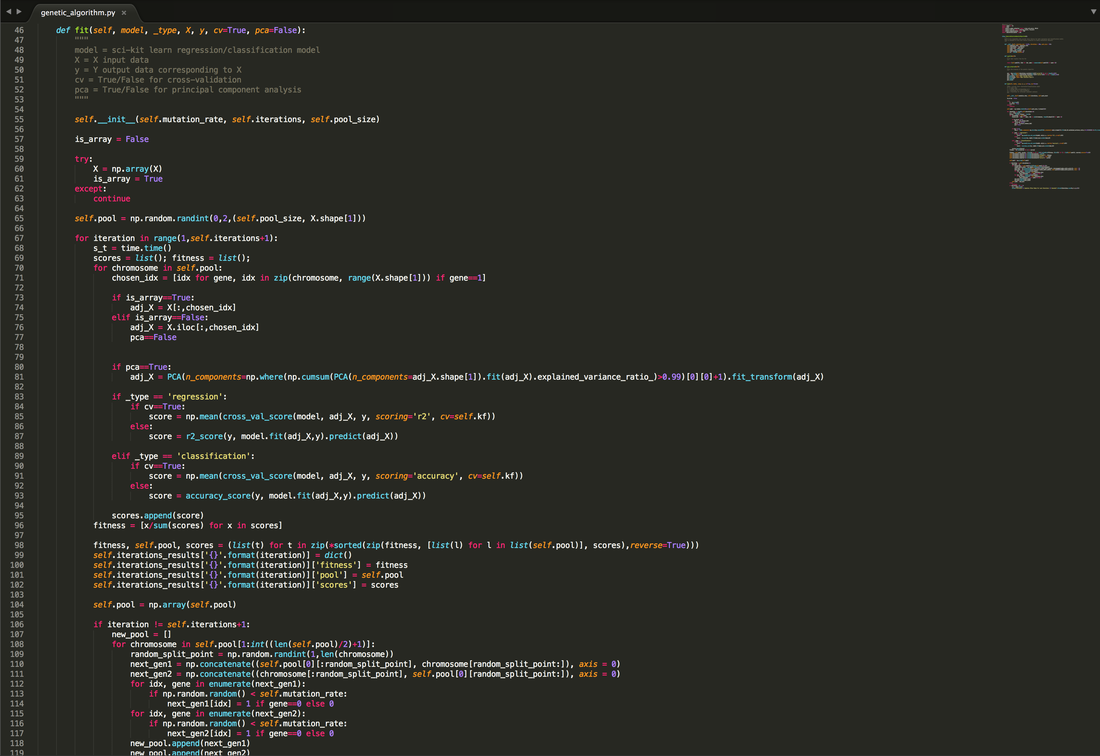
The fit method is the main method in the class. I have used this terminology to fall in line with sci-kit learn's library seeing as this is a very familiar and well known approach amongst the python community.
fit() Method - Stage 1 - init & Pool Generation
The first stage of the method begins by re-initialising the instance so that the hyperparaemters and the pool are clear for a new fit. The input X dataset is then converted into a numpy array as this runs more efficiently. If this conversion fails, it assumes that the data used in a panads dataframe. Being able to support both is important, however, if the dataframe contains non-numerical data, then this cannot be used in Principal Component Analysis and is therefore the PCA parameter is disabled later in the method should the conversion fail.
A random pool of solutions is then generated using a number of numpy arrays filled with 1s and 0s the length of how ever many features there are to select from. The size of this pool is taken from the "pool_size" hyperparameter stated when initiating the instance. Once that is all set, the algorithm will begin to score each of the solutions to see which is the best fit.
fit() Method - Stage 2 - PCA, Cross Validation & Fitness
The second part of the method looks at each solution/chromosome and scans it to see which features the solution/chromosome says should be selected by looking at the genes. From this, an adjusted dataset with those selected columns is formed.
If the user has decided that they would like to apply PCA, then the method looks at the adjusted dataset and applies PCA to all columns of the adjusted dataset in order to then select the number of features that should be applied to transform the dataset ensuring that at least 99% of the variance is captured by the transformation. This is to ensure that not too much information is lost in an attempt to reduce the effects of dimensionality.
The method then scores the model fitted to the adjusted dataset. For regression models, they are scored based on their "r-squared" score and for classification models, they are scored based on their "accuracy" score. I have added a hyperparameter to enable cross-validation, using K-Fold cross-validation with a value of K=5. This is to ensure that the scores provided take overfitting into account. The average of the 5 scores is returned. If the user does not wish to cross-validate, then the option is there, and a direct score of the model trained against the whole dataset is provided, although this is not advised. A fitness score based on the score of the solution in comparison to the rest of the solutions is then calculated to then rank the pool of solutions in order of the best.
fit() Method - Stage 3 - Storing Results
This stage stores all the results so that each iteration can be accessed to analyse. These scores are held within the object itself as a dictionary and are callable as an attribute within the instance. These are reset and repopulated every time the fit() method is called.
fit() Method - Stage 4 - Reproducing & Mutation
This part of the algorithm focuses on reproducing the best solutions in order to come up with a better pool. To do this, it gets rid of the bottom half of the solutions that scored poorly, then reproduces the best solution from the pool with the remaining of the population to create a brand new generation. The reproduction of the best solution and all remaining solutions is done by randomly selecting a point along the pair of chromosomes and swapping the remaining genes along the pair of chromosomes beyond that point.
Following the reproduction of the chromosomes, the genes along the chromosomes have a probability of mutating (switching from 0 to 1 or vice versa), this probability is the "mutation_rate" variable stated when initiating the instance. Once that is complete, a new pool of solutions is generated and then scored again and reproduced again and so forth for as many iterations specified at the initiating of the instance.
Other Methods
I have added a couple of other methods that can help to extract information from running the algorithm. I have added a "results()" method which returns the optimal solution from the pool of solutions in the form of a tuple where the first value of the tuple is an array of the gene sequence indicating which columns to select and the second is a list of indexes that should be selected to reflect the gene sequence where the gene/feature is equal to 1.
I have also added a "plot_progress()" function where you're able to see the algorithm results at each iteration.
Performance Review
I tested this using a sample the infamous digits recognising data. For those that are unfamiliar, this is a dataset containing 8x8 images of hand-written digits and their corresponding values. Using the pixels of the image as features (8*8 = 64 features), you are tasked with predicting what number it is.
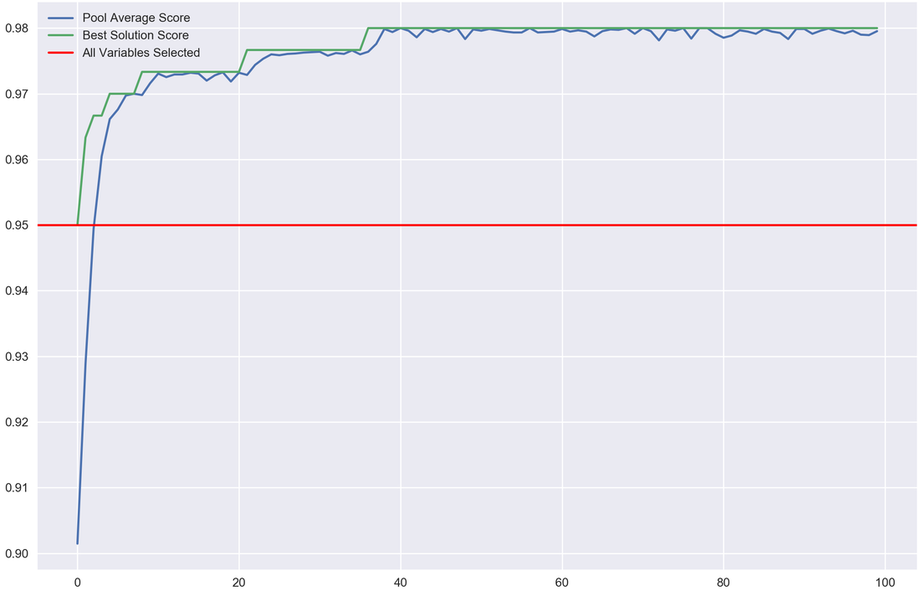
I tested this using scikit-learn's logistic regression model. I ran a cross-validated scoring of the model while selecting all the features and it came to 95%, which on its own is quite impressive without any pre-processing. I then ran this with the genetic algorithm and managed to get a score of 98%. Though incrementally better, this provides confidence that this approach is worth exploring and expanding on which I aim to do in future.
I tested this using scikit-learn's logistic regression model. I ran a cross-validated scoring of the model while selecting all the features and it came to 95%, which on its own is quite impressive without any pre-processing. I then ran this with the genetic algorithm and managed to get a score of 98%. Though incrementally better, this provides confidence that this approach is worth exploring and expanding on which I aim to do in future.
Next Steps...
Moving forward, I would like to be able to publish this code in a more professional manner that is in line with coding standards amongst the developer world. I come from a mathematical background and have limited developer standards knowledge, so this will help break into that.
I would also like to develop the fitness scores so that it takes into account F scores, recall scores, and looks to add regularisation to minimise the number of features used as well as take into account p-values in regression models in order to maximise significance within features.
I am also looking to implement the ability to add transformations into the algorithms. This adds a layer of complexity and a potential better dataset by allowing a feature to be selected or not (ie. 1 or 0) and then to be transformed in some way (eg. log(x+1)) as well as having the option to mutate this transformation.
I would also like to develop the fitness scores so that it takes into account F scores, recall scores, and looks to add regularisation to minimise the number of features used as well as take into account p-values in regression models in order to maximise significance within features.
I am also looking to implement the ability to add transformations into the algorithms. This adds a layer of complexity and a potential better dataset by allowing a feature to be selected or not (ie. 1 or 0) and then to be transformed in some way (eg. log(x+1)) as well as having the option to mutate this transformation.